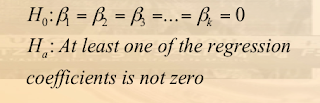Theory revision 2

• population
• it is a collection of possible individuals, objects or measurement of interest
• example: population of Australia.
• sample
• it is a portion or part of the population of interest
• example: 30 of UTS students
• parameter
• it is a measurable characteristic of a population
• example: total population of Melbourne
• statistic
• it is a measurable characteristic of a sample.
• example: 15 of wine lovers
• statistical inference
• it is the process of drawing conclusion from data subject to random variation such as observational errors and sample variation.
• example: 15 percent of beer lovers

Theory revision 1

• Statistic is the science of collecting, organizing, presenting, analyzing and interpreting numerical data to assist in making more effective decision. This technique is used extensively by marketing, accounting, quality control, consumers, professional sports people, hospital administrators , educators, politician and so on,
• Descriptive statistics is the methods of organizing, summarizing and presenting data in an informative way.
• Inferential statistics is a decision, estimate, prediction or generalization about a population, based on sample.
• Qualitative data is the characteristic or variable being studied is non numeric.
• Quantitative data is the variable that can be reported numerically.
• A population is a collection of possible individuals, objects or measurement of interest.
• A sample is a portion or part of the population of the interest.

Homoscedasticity

In statistics, a sequence or a vector of random variables is homoscedastic, if all random variables in the sequence or vector have the same finite variance.

Theory revision 5

The multiple standard error of estimate is a measure of the effectiveness of the regression equation.

• It is measured in the same units as the dependent variable.
• It is difficult to determine what is a large value and what is a small value of the standard error.
• The independent variables and the dependent variable have a linear relationship.
• The dependent variable must be continuous and at least interval scale.
• The variation in (Y-Y') or residual must be the same for all values of Y. When this is the case, we say the difference exhibits homoscedaticity.
• A residual is the difference between the actual value of Y and the predicted value Y'.
• Residuals should be approximately normally distributed, Histograms and stem and leaf charts are useful in checking this requirement.
• The residuals should be normally distributed with mean 0.
• Successive values of the dependent variable must be uncorrelated.

The ANOVA table 

• The ANOVA table gives the variation in the dependent variable(of both that which is and is not explained by the regression equation),
  
• It is used as a statistical technique or test in detecting the differences in population means or whether or not the means of different groups are all equal when you have more than two population.

Correlation Matrix 

• A correlation matrix is used to show all possible simple correlation coefficients between all variables.
• the matrix is useful for locating correlated independent variables.
• How strongly each independent variable is correlated to the dependent variable is shown in the matrix.

Global Test 

• The global test is used to investigate whether any of the independent variables have significant coefficients. 
• The test statistic is the F distribution with k (number of independent variables) and n-(k+1) degree of freedom, where n is the sample size.

Test for individual variables

• This test is used to determine which independent variables have non zero regression coefficient.
• The variables that have zero regression coefficients are usually dropped from the analysis.
• The test statistic is the t distribution with n-(k+1) degrees of freedom.

Qualitative Variables and Stepwise Regression

• Qualitative variables are non numeric and also called dummy variables
• For a qualitative variable, there are only two conditions possible.
• Stepwise Regression leads to the most efficient regression equation
• Only independent variables with significant regression coefficients are entered into the analysis. Variables are entered in the order in which they increase R^2 the fastest.

Theory revision 4

Hypothesis Testing

• Testing hypothesis is an essential part of statistical inference.
• A statistical hypothesis is an assumption about a population. This assumption may or may not be true.
• For example, claiming that a new drug is better than the current drug for treatment of the same symptons.
• The best way to determine whether a statistical hypothesis is true would be to examine the entire population.
• Since that is often impractical, researchers examine a random sample from the population.If sample data are consistent with the statistical hypothesis, the hypothesis is accepted if not, it is rejected.
• Null Hypothesis: the null hypothesis denoted by H0 is usually the hypothesis that sample observations result purely from chance.
• Alternative Hypothesis: The alternative hypothesis denoted by H1 is the hypothesis that sample observations are influenced by some non random cause.
• Statisticians follow a formal process to determine whether to accept or reject a null hypothesis based on sample data. This process, called hypothesis testing consists of five steps.
1. State null and alternative hypothesis
2. write down relevant data, select a level of significance
3. Identify and compute the test statistic, Z to be used in testing the hypothesis.
4. Compute the critical values Zc.
5. Based on the sample arrive a decision.
• Decision errors
• Type I error: A type I error occurs when the null hypothesis is rejected when it is true. Type I error is called the significance level. This probability is also denoted by Alpha. α
•  Type II error: A type II error occurs when the researcher accepts a null hypothesis that is false.
•  One-tailed and two-tailed tests
• A test of a statistical hypothesis, where the region of rejection is on only one side of the sampling distribution is called a one tailed test.
• For example, suppose the null hypothesis states that the mean is equal to or more than 10. The alternative hypothesis would be that the mean is less than 10.
• The region of rejection would consist of a range of numbers located on the left side of sampling distribution that is a set of numbers less than 10.
• A test of a statistical hypothesis where the region of rejection is on both sides of the sampling distribution is called a two tailed test.
• For example, suppose the null hypothesis would be that the mean is equal to 10, the alternative hypothesis would be that the mean is less than 10 or greater than 10.
• The region of rejection would consist of a range of numbers located on both sides of sampling distribution; that is the region of rejection would consist partly of numbers that were less than 10 and partly numbers that were greater than 10.
• Degree of freedom
• The concept of degree of freedom is central to the principle of estimating  Statistics of population from samples of them.
• It is the number of scores that are free to try.

Theory revision 3

Bernuolli Trials 

• Random with two outcomes (success or failure)
• Random variable X often coded as 0(failure) and 1(success)
• Bernoulli trail has probability of success usually denoted p.
• Accordingly probability of failure (1-p) is ususally denoted
• q=1-p
• where x can be zero or one.
• probability of Bernoulli Distribution is;  
  

Binomial distribution

1. identical number of trials
2. the binomial distribution which consists of a fix number of statistically independent BErnoulli trials.
3. 2 possible outcome for each trials(success or failure)
4. each trial is independent(does not affect the others)
5. probability of success is the same for each trial
6. Shapes of binomial distribution
• if p<0.5: the distribution will exhibit positive skew
• if p=0.5: the distribution will be symmetirc
• if p>0.5: the distribution will exhibit negative skew

Poisson Random Variable 

• Poisson random variable represents the number of independent events that occur randomly over unit of times.
• Count number of times as event occur during a given unit of measurement.
• Number of events that occur in one unit is independent of other units.
• Probability that events occurs over given unit is identical for all units.(constant rate)
• Events occur randomly
• Expected number of events(rate) in each unit is denoted by λ(lambda)

Residual Plpt

Analysis of Residuals

• A residual is the difference between the actual value of Y and the predicted value Y'.
• Residual should be approximately normally distributed. Histograms and stem and leaf chars are useful in checking this requirement.
• A plot of the residuals and their corresponding Y' values is used for showing that there are no trends or patterns in the residuals.

Qualitative Variables & Stepwise Regression

• Qualitative variables are non-numeric and are also called dummy variables.
• For a qualitative variable, there are only two conditions possible
• Stepwise Regression leads to the most efficient regression equation.
• Only independent variables with significant regression coefficients are entered into the analysis. Variables are entered in the order in which they increase R^2 the fastetst.

Test for individual variables

• This test is used to determine which independent variables have non zero regression coefficients.
• The variables that have zero regression coefficients are usually dropped from the analysis.
• The test statistic is the t distribution with n-(k+1) degrees of freedom.

Global Test

• The global test is used to investigate whether any independent variables have significant coefficients. The hypotheses are:

The test statistic is the F distribution with k ( number of independent variables) and n(k+1) degrees of freedom, where n is the sample size.

Correlation Matrix

• A correlation matrix is used to show all possible simple correlation coefficients between all variables.
• The matrix is useful for locating correlated independent variables.
• How strongly each independent variable is correlated to the dependent variable is shown in the matrix.

The ANOVA table

• The ANOVA table gives the variation in the dependent variable ( of both that which is and is not explained by the regression equation).
• It is used as a statistical technique or test in detecting the differences in population means or whether or not the means of different groups are all equal when you have more than two populations.

Multiple Regression and Correlation

• The independent variables and the dependent variable have a linear relationship.
• The dependent variable must be continuous and at least interval-scale.
• The variation in (Y-Y') or residual must be the same for all values of Y. When this is the case, we say the difference exhibits homoscedasticity.
• The residuals should be normally distributed with mean 0.
• Successive values of the dependent variable must be uncorrelated.

Multiple Standard Error of Estimante

• The multiple standard error of estimate is a measure of the effectiveness of the regression equation.
• It is measured in the same units as the dependent cariable.
• It is difficult to determine what is a large value and what is a small value of the standard error.
• The formula is 

• where n is the number of observations and k is the number of independent variables.

Multiple Regression Analysis

• For two independent variables, the general form of the multiple regression equation is
• Y'=a+b1X1+b2X2
• X1 and X2 are the independent variables.
• a is the Y intercept
• b1 is the net change in Y for each unit change in X1
• holding X2 constant. It's called a partial regression coefficient a net regression coefficient or just a regression coefficient.
• The general multiple regression with k independent variable is givien by:
• The least squares criterion is used to develop this eauation.
• Calculating, b1, b2, etc is very tedious there are many computer software packages that can be used to estimate these parameters

Regression Analysis

• Purpose: to determine the regression equation; it is used to predict the value of the dependent variable (Y) based on the independent variable (X). 
• Procedure: select a sample from the population and list the paired data for each observation; draw a scatter diagram to give a visual portrayal of the relationship; determine the regression equation.
• The regression line 
• A straight line that represents the relationship between two variables 
• Useful to add to the scatterplot to help us see the direction of the relationship 
• But it’s much more than this… 
• Prediction 
• Regression line enables us to predict Variable Y on the basis of Variable X

• b 
• The slope of the regression line 
• The amount of change in Y associated with a one-unit change in X
•  a 
• The intercept 
• The point where the regression line crosses the Y axis 
• The predicted value of Y when X = 0

Rank Order Correlation

• The correlation coefficient(r) is based on the assumption that data is normally distributed.
• If the data are skewed, instead of r we use a rank order correlation rs (also called spearman coefficient) as follows.

• Where d=difference between the ranks of each pair
• N=the number of pair of observations
• The spearman coefficient will assume any value between -1.00 to + 1.00 inclusive.
• -1.00 indicates a perfect negative correlation
• +1.00 indicates a perfect positive correlation
• The ranking order has to be done for each pair of data
• The highest data value will be lowest rank or the other way.
• The lowest data value will be highest rank or the other way.

t value

• with (n-2) degree of freedom
• df= number of points on scatter plot minus 2

Formula for correlation coefficient (r)

Strong Positive Correlation

Zero Correlation

Perfect Positive Correlation

Perfect Negative Correlation

The coefficient of correlation, r

• The Coefficient of Correlation (r) is a measure of the strength of the relationship between two variables. It requires interval or ratio-scaled data (variables). 
• It can range from -1.00 to 1.00. 
• Values of -1.00 or 1.00 indicate perfect and strong correlation. 
• Values close to 0.0 indicate weak correlation. 
• Negative values indicate an inverse relationship and positive values indicate a direct relationship

Correlation Analysis

• Correlation Analysis: A group of statistical techniques used to measure the strength of the relationship (correlation) between two variables.
• Scatter Diagram: A chart that portrays the relationship between the two variables of interest.
• Dependent Variable: The variable that is being predicted or estimated. 
• Independent Variable: The variable that provides the basis for estimation. It is the predictor variable.

The Chi Square Distribution

• The chi square distribution is asymmetric and its values are always positive.
• Degrees of freedom are based on the table and are calculated as (rows-1)X(columns-1). Or just (rows-1)

What your table should like

Chi-square Hypothesis Testing

The major characteristics of the chi-square distribution are

• It is positive skewed
• It is non-negative
• It is based on degrees of freedom
• When the degrees of freedom change a new distribution is created

Hypothesis testing consists of five steps.

• State Null and alternative hypothesis
• Write down relevant data, select a level of significance
• Identify and compute the test statistic x2 to be used in testing they hypothesis.
• Compute the Critical values x2 C
• Based on the sample arrive a decision
• Use the following formula for test stastistic x2 values as follows:



• Where f0 is the observed frequency and fe is the excepted frequency
• Then the critical values are determined
• Chi-square distribution is a family of distribution but each distribution has a different shape depending on the degrees of freedom, df.
• The data are often presented in a table format. if starting with raw data on two variables, a table must be created first.
• Columns are scores of the independent variable.
• There will be as many columns as there are scores in the independent variable.
• Rows are scores of the dependent variable.
• There will be as many rows as there are scores on the dependent variable.

Hypothesis Testing

Introduction

• Testing hypothesis is an essential part of statistical inference
• A statistical hypothesis is an assumption about a population. This assumption may or may not be true.
• For example, claiming that a new drug is better than the current drug for treatment of the same symptoms.
• The best way to determine whether a statistical hypothesis is true would be to examine the entire population.
• Since that is often impractical, researchers typically examine a random sample from the population. If sample data are consistent with the statistical hypothesis, the hypothesis is accepted; if not, it is rejected.

There are two types of statistical hypotheses

• Null Hypothesis

• The null hypothesis denoted by H0, is usually the hypothesis that sample observations result purely from chance. 
• H0:=
• H1:≠ : two-tail test
• H1:</> : one-tail test

• Alternative Hypothesis 

• The alternative hypothesis, denoted by H1 is the hypothesis that sample observations are influenced by some non-random cause.
• H1 or Ha
• For example, suppose we wanted to determine whether a tossing a coin was fair and balanced, A null hypothesis might be that half the flips would result in heads and half in tails. The alternative hypothesis might be that the number of heads and tails would be very different. symbolically there hypotheses would be expressed as
• H0:P = 0.5
• Ha:P ≠ 0.5
• Statisticians follow a formal process to determine whether to accept or reject a null hypothesis, based on sample data. This process called hypothesis testing, consists of five steps
1. State Null and alternative hypothesis (based on population mean.)
2. Write down relevant data, select a level of significance;α (rejection area)
3. Identify and compute the test statistic Z to be used in testing the hypothesis.
4. Compute the Critical values(the line which is between rejection area and non rejection area) (boundary) Zc
5. Based on the sample arrive a decision

Use the following formula for test statistic/Z value as follows

• if the standard diviation is  known
• number of sample>30

Remember this formula is for Testing Hypotheses about Single Means when the poplation Variance is known.
But when the population variance is unknown, we must use the standard deviation s, to estimate σ
We use t distribution instead of Z distribution.

• if the standard deviation is unknown
• number of sample < 30

Decision Errors

• Two types of errors can result from a hypothesis test.
• Type I error: A type I error occurs when the null hypothesis is rejected when it is true. Type I error is called the significance level. This probability is also denoted by alpha, α.
• Type II error: A type II error occurs when the researcher accepts a null hypothesis that is false. H0 is accepted. 

Null Hypothesis	Accept H0	Reject H0
H0 isTRUE	Correct Decision	Type I error
H0 is FALSE	Type II error	Correct Decision

One-Tailed Tests

• A test of a statistical hypothesis where the region of rejection is on only one side of the sampling distribution, is called a one tailed test.
• For example suppose the null hypothesis states that the mean is equal to or more than 10. The alternative hypothesis would be that the mean is LESS than 10.
• The region of rejection would consist of a range of numbers located on the LEFT side of sampling distribution, that is a set of numbers LESS than 10.

Two-Tailed Tests 

• A test of a statistical hypothesis, where the region of rejection is on both sides of the sampling distribution, is called a two-tailed test.
• For example, suppose the null hypothesis states that the mean is equal to 10. The alternative hypothesis would be that the mean is less than 10 or greater than 10.
• The region of rejection would consist of a range of numbers located on both sides of sampling distribution; that is the region of rejection would consist party of numbers that were less than 10 and partly of numbers that were greater than 10.

df=degree of freedom =n-1

The concept

• The concept of degrees of freedom is central to the principle of estimating statistics of populations from samples of them
• The number of scores that are free to vary
• In many situations, the degrees of freedom are equal to the number of observations minus one.
• Used if the sample number is LESS than 30.

Confidence Interval for a population proportion

95% and 99% Confidence Intervals for µ

• The 95% and 99% Confidence Intervals for µ are constructed as follows when n>30 
• 95% CI for the population mean is  given by 
  
• 99% CI for the population mean is given by
  
• In general a confidence interval for the population mean is computed by
  

Standard Error of the Sample Means

• The standard error of the sample means is the standard deviation of the sampling distribution of the sample means.
• it is computed by 

General Concepts of Estimation

Point estimate

A point estimate is one value ( a point) that is used to estimate a population parameter.

Examples of point estimates are the sample mean, the sample standard deviation, the sample variance, the sample proportion etc...

EXAMPLE: The number of defective items produces by a machine was recorded for five randomly selected hours during a 40-hour work week, The observed number of defectives were 12, 4, 7, 14 and 10. So the sample mean is 9.4  thus a point estimate for hourly mean number of defectives is 9.4.

 Interval Estimate

• An Interval Estimate states the range within a population parameter probably lies. 
• The  interval within a population parameter is expected to occur is called a confidence interval.
• The  two confidence intervals that are used extensively are the 95% and the 99%
• The confidence level describes the uncertainty associated with a sampling  method.
• Suppose we used the same sampling method to select different samples and to compute a different interval estimate for each sample. some interval estimates would include the true population parameter and some would not. A 90% confidence level means that we would expect 90% of the interval estimates to include the population parameter.
• A 95% confidence interval means 95% of the sample means for a specified sample size will lie within 1,96 standard deviations of the hypothesized population mean.
• For the 99% confidence interval, 99% of the sample means for a specified sample size will lie within 2.58 standard deviation of the hypothesized population mean.

Statistical Inference

• Statistical inference refers to the use of information obtained from a sample in order to make decisions about unknown quantities in the population of interest.
• Since all population may be characterized or fully described by their parameters, it is important to make inferences on the one or more parameters whose values are unknown
• There are two main types of inferences
1. The hypothesis testing branch involves making decisions concerning the value of a parameter by testing a per-conceived hypothesis.
2. The estimation branch involves estimating or predicting the unknown value of a parameter.
• Both approaches involves the use of sample information in the form of sample statistic corresponding to the population parameter in question.
• Both approaches also rely on the "goodness" of the inference, which requires complete knowledge of the sampling distribution.

Estimation

• Up to this point we have assumed that the parameters of the population of interest are unknown.
• When dealing with methods such as normal distribution, the population mean, µx and standard deviation σx were given.
•  In estimation, there is a complete change in the type of problem with which we are concerned.
• Now we have to get used to dealing with problems where the population parameter of interest is either completely unknown or is given as a hypothetical(assumption) value. Solving these problem involves statistical inference.
• The general concepts of estimation
  1. θ represent any parameter of interest. e.g. the parameter whose value is unknown and must be estimated.
  2. Ô sample statistic that will be used to estimate unknown θ. 
  3. σÔ represents the standard error sample statistic,Ô. This measures the variability or error associated with all possible values of Ô as an estimate of θ
• There are two possibilities of determining population parameters - we can either calculate it exactly or we can estimate it.

Empirical Rule

Applies to mound shaped and symmetric probability density.

• P (µ - σ < X <µ + σ) = 0.68 
• P (µ - 2σ < X <µ + 2σ) = 0.95 
• P (µ - 3σ < X <µ + 3σ) = 0.997

Random Variable

• A random variable represents a possible outcome (usually numeric) from a random experiments&amp
  • Let X be random variable for a number of heads in 3 coin flips 
  • X represents any value from sample space {0, 1, 2 or 3)
• An observation is a realization of random variable
  • Let x be an observed number of heads in 3 coin tosses, eg x = 0

Bernuolli Trials:

• Random trial with two outcomes. Eg. Success or Failure. 
• Random variable X often coded as 0 (Failure) and 1 (Success)
• Bernuolli Trail has probability of success usually denoted p. Eg. P (Success) = p (x =1) = p 
• Accordingly, probability of failure (1 – p) is usually denoted q = 1 - p. 
• Eg. p (Failure) = 1 – p = q 
• Probability of Bernuolli’s Distribution is: 
• Where x can be zero or one
• The Binomial Distribution which consists of a fixed number of statistically independent Bernoulli trials

Binomial Distributing Function:

Poisson Random Variable:

Poisson random variable represents the number of independent events that occur randomly over unit of times 

Example:

• Number of calls to a call centre in an hour 
• Number of floods in a river in a year 
• Number of misprint in a page

Characteristic:

• Count number of times as event occur during a given unit of measurement (e.g. time, area). 
• Number of events that occur in one unit is independent of other units. 
• Probability that events occurs over given unit is identical for all units (constant rate) 
• Events occur randomly 
• Expected number of events (rate) in each unit is denoted by λ (lambda)

Poisson Distribution:

• Let x be Poisson random variable for number of independent events over unit of measurements. 
• To define probability distribution need to know: rate of unit occurrence per unit - λ .

Probability

Notion of probability:

• An event is a particular result or set of results
• A possibility space is the set of all possible outcomes
• Fro equally likely outcomes, the probability of an event E is given by

Compound event probability:

"A measure of the likely-hood that a compound event will occur" Method of calculating compound event probability

• Formulas
  • Additive rule
  • Conditional probability formula
  • Multiplicative rule
• Venn Diagram and Tree Diagram

Additive rule:

Mutually exclusive events:

• Both events cannot occur at the same time
  • Both male and female for one person
  • Both heads and tails for one coin toss
• No sample points in common(overlap)
  • All female students who are Muslim in room 102
  • All male students who are Christian in class room 103

Therefore probability of mutually exclusive events happening together is 0

Example:

additive rules for mutually exclusive events:

conditional probability

"probability of one event occurring given that another event has occurred"

Characteristics

• Restrict original sample space to account for new information
• Assumes probability of given event ≠ 0

Conditional probability:

P( B | A ) represents the probability of event B occurring given that event A has already occurred.
Suppose we draw two cards from a deck of 52.
Find the probability that the second card is a Jack given that the first card was a Jack and it was not replaced.
P( J2 | J1 ) = 3/51 ≈ 0.059
Find the probability that the second card is a Jack given that the first card was a Jack and it was replaced.
P( J2 | J1 ) = 4/52 = 1/13 ≈ 0.077

We can use the Multiplication Rule to calculate the probability of consecutive events.
 P( A and B ) = P(A) ∙ P( B | A )
 If events A and B are independent, then
P( A and B ) = P(A) ∙ P(B)

Conditional probability using Venn diagram:

Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets (aggregation of things). Venn diagrams were conceived around 1880 by John Venn. They are used to teach elementary set theory, as well as illustrate simple set relationships in probability, logic, statistics, linguistics, and computer science.

Multiplicative rule: 

Independent events:

"The occurrence of one event does not influence the probability of another event"

To test for independence:

• P (A|B) = P (A)
• P (B|A) = P (B)
• P (A ∩ B) = P (A) * P (B)

Tree Diagram:

"A branched picture of multiplicative rule and used for finding (A ∩ B)”

Characteristics:

• Each set of branches is an event 
• Each set of branches should add up to 1 
• Multiply along each branch to find the probability of particular event

Example:
In a certain clothing shop, 40% of shoppers try on a jacket when browsing. Of those who try on jacket, 70% will subsequently purchase a jacket. However, 15% of browsers buy a jacket without trying on. What is the probability that a person who buys a jacket has tried one on?
Solution: Tree diagram
Let, Event (A) = customer tries on a jacket
       Event (B) = Customer buys a jacket First,
Find P(A) and then P(A|B)

Measures of Dispersion

Range:

The difference between the largest and the smallest numbers in the dataset.
The disadvantage of using range is that it does not measure the spread of the majority of valuses in a data set. It only measures the spread between highest and lowest values.

The Interquartile Range:

 The difference between the lower quartile and the upper quartile in the data set.

• Example:
• 87, 88, 88, 89, 90, 90, 90, 92, 93, 93, 95
• The Mean is the sixth value, 90
• Now consider the lower half of the data which is 87, 88, 88, 89, 90 and the middle of this set called lower quartile Q1 = 88
• The upper half of the set is 90, 92, 93, 93, 95 and the middle, called the upper quartile, Q3= is 93
• Therefore the interquartile is
• IQR = Q3 –Q1 =93 -88 = 5

Quartile Deviation:

half the distance between the third quartile, Q3, and the first quartile.
 QD = [Q3 - Q1]/2

Box Plots:

A graphical display based on quartiles that helps to picture a set of data.
Five pieces of data are needed to construct a box plot:

• The minimum Value
• The first quartile
• The median
• The third quartile
• The maximum value

Mean Deviation:

Another method for indicating the spread of results in data set.
Determine the average mean and the average value of the deviation of each score from the mean.
Thus each data point is taken into account
The average of the absolute values of the deviations from mean

Steps

• Find the mean or median or mode of the given series
• Using and one of three, find the deviation(Differences) of the items of the series from them
• Find the absolute values of these deviations e.g. ignore there positive or negative signs
• Find the sum of these absolute deviations and find the mean deviation

Variance:

A measure of how spread out a data set is. It is calculated as the average squared deviation of each number from the mean of a data set.
Variance(S2)=average squared deviation of values from mean.

Standard deviation:

• The measure of spread most commonly used in statistical practice when the mean is used to calculate central tendency.
• Thus it measures spread around the mean. Because of its close links with the mean, standard deviation can be greatly affected if the mean gives a poor measure of central tendency
• Standard deviation is also useful when comparing the spread of two separate data sets that have approximately the same mean.
• The data set with the smaller standard deviation has a narrower spread of measurements around the mean and therefore usually has comparatively fewer high or low values
• The standard deviation for a discrete variable made up of n observations is the positive square root of the variance and is defined as
  
  

Steps:

• Calculate the mean/li>
• Subtract the mean from each observation
• Square each of resulting observations
• Add these squared results together
• Divide this total by the number of observations(variance S2)
• Use the positive square root(standard deviation,S)

Standard Deviation from frequency table: 

Coefficient of Variation:

This is the ratio of the standard deviation to the mean:

To compare the variations(dispersion) of two different series.