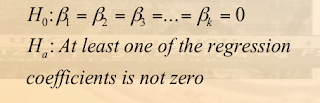- It is measured in the same units as the dependent variable.
- It is difficult to determine what is a large value and what is a small value of the standard error.
- The independent variables and the dependent variable have a linear relationship.
- The dependent variable must be continuous and at least interval scale.
- The variation in (Y-Y') or residual must be the same for all values of Y. When this is the case, we say the difference exhibits homoscedaticity.
- A residual is the difference between the actual value of Y and the predicted value Y'.
- Residuals should be approximately normally distributed, Histograms and stem and leaf charts are useful in checking this requirement.
- The residuals should be normally distributed with mean 0.
- Successive values of the dependent variable must be uncorrelated.
The ANOVA table
- The ANOVA table gives the variation in the dependent variable(of both that which is and is not explained by the regression equation),
- It is used as a statistical technique or test in detecting the differences in population means or whether or not the means of different groups are all equal when you have more than two population.
Correlation Matrix
- A correlation matrix is used to show all possible simple correlation coefficients between all variables.
- the matrix is useful for locating correlated independent variables.
- How strongly each independent variable is correlated to the dependent variable is shown in the matrix.
Global Test
- The global test is used to investigate whether any of the independent variables have significant coefficients.
- The test statistic is the F distribution with k (number of independent variables) and n-(k+1) degree of freedom, where n is the sample size.
Test for individual variables
- This test is used to determine which independent variables have non zero regression coefficient.
- The variables that have zero regression coefficients are usually dropped from the analysis.
- The test statistic is the t distribution with n-(k+1) degrees of freedom.
Qualitative Variables and Stepwise Regression
- Qualitative variables are non numeric and also called dummy variables
- For a qualitative variable, there are only two conditions possible.
- Stepwise Regression leads to the most efficient regression equation
- Only independent variables with significant regression coefficients are entered into the analysis. Variables are entered in the order in which they increase R^2 the fastest.